Uppgift 3.1(Appl): 3. Lösningskurvor
Differentialekvationen:
 |
(1.1) |
Begynnelsedata:
 |
(1.2) |
Lösningen:
 |
(1.3) |
Här är det lämpligt att definiera en funktion av både x och p.
 |
(1.4) |
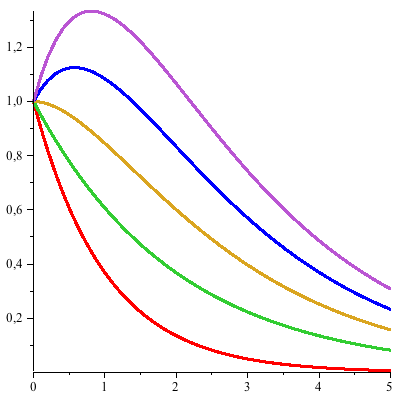
En familj av lösningar där 
varierar mellan -1 och 1 med steglängden 1/2 genereras med funktionen seq.
 |
(1.5) |
Graferna ritas sedan med plotfunktionen.
 |