Uppgift 4.2: 31
Potentialvandring i de två nätmaskorna ger ekvationerna
![`+`(`*`(L, `*`((D(i[1]))(t))), `*`(R[1], `*`(`+`(i[1](t), `-`(i[2](t))))), `-`(E)) = 0, `+`(`/`(`*`(i[2](t)), `*`(C)), `*`(`+`(R[1], R[2]), `*`((D(i[2]))(t))), `-`(`*`(R[1], `*`((D(i[1]))(t))))) = 0](images/datorle3_56.gif){kind=small} |
(4.1) |
Om numeriska data samlas i en mängd blir kalkylen överskådligare
![{L = 2, C = `/`(1, 125), R[1] = 50, R[2] = 25, E = 100}](images/datorle3_58.gif){kind=small} |
(4.2) |
Begynnelsedata
 = 0, i[2](0) = 0](images/datorle3_60.gif){kind=small} |
(4.3) |
Differentialekvationen med numeriska data på komponenterna
![`+`(`*`(2, `*`((D(i[1]))(t))), `*`(50, `*`(i[1](t))), `-`(`*`(50, `*`(i[2](t)))), `-`(100)) = 0, `+`(`*`(125, `*`(i[2](t))), `*`(75, `*`((D(i[2]))(t))), `-`(`*`(50, `*`((D(i[1]))(t))))) = 0](images/datorle3_62.gif){kind=small} |
(4.4) |
har med givna begynnelsevillkor lösningen
 = `+`(2, `*`(`/`(1, 10), `*`(exp(`+`(`-`(`*`(5, `*`(t))))), `*`(`+`(`*`(40, `*`(`^`(6, `/`(1, 2)), `*`(sin(`+`(`*`(`/`(5, 3), `*`(`^`(6, `/`(1, 2)), `*`(t)))))))), `-`(`*`(20, `*`(cos(`+`(`*`...](images/datorle3_64.gif){kind=small} |
(4.5) |
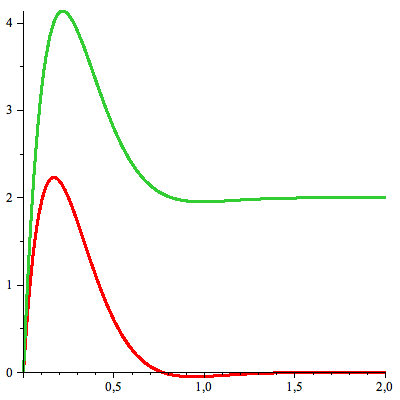
Lösningarna ritas på vanligt sätt
 |