Uppgift 5.4: 28 (Resolventmatris) 

restart; -1; with(inttrans); -1; with(LinearAlgebra); -1 

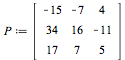
`:=`(P, Matrix(%id = 21935128)) 

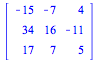Matrix(%id = 22419480) (4.1)
 

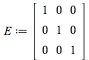
`:=`(E, Matrix(%id = 3047120)) 

Matrix(%id = 3717008) (4.2)
 

`:=`(lambda, T, Eigenvectors(P)) 

Vector[column](%id = 7673432), Matrix(%id = 7673504) (4.3)
 

Resolventmatrisen. 

`:=`(R, MatrixInverse(`+`(`*`(s, `*`(E)), `-`(P)))) 

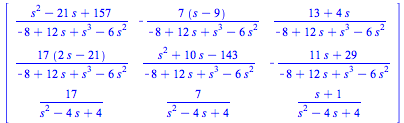Matrix(%id = 6765744) (4.4)
 

Här använder vi map-funktionen för att lÃ¥ta invlaplace verka pÃ¥ matriselemeten i resolventmatrisen för att beräkna fundamentalmatrisen = exponentialmatrisen. 

`:=`(X, map(invlaplace, R, s, t)) 

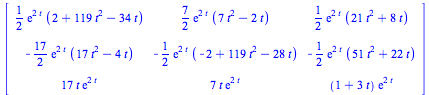Matrix(%id = 5035476) (4.5)
 

Allmänna begynnelsedata 

`:=`(b, Vector[column](%id = 7031172)) 

Vector[column](%id = 6964804) (4.6)
 

ger lösningsvektorn 

`:=`(x, Typesetting:-delayDotProduct(X, b)) 

Vector[column](%id = 3519252) (4.7)
 

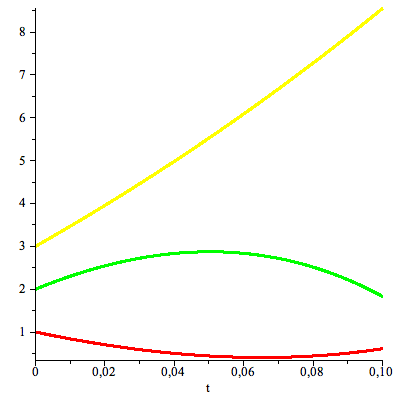
Med speciella värden fÃ¥r vi i stället möjlighet att rita graferna till lösningsvektorns komponenter. 

`:=`(b, Vector[column](%id = 7026204)) 

Vector[column](%id = 22280952) (4.8)
 

plot(Typesetting:-delayDotProduct(X, b), t = 0 .. `/`(1, 10), thickness = 2) 

Plot_2d