Uppgift 6.2: 31
 |
(2.1) |
 |
(2.2) |
Bestäm jämviktspunkterna
  |
(2.3) |
Det är förstås bara de reella värdena som är intressanta.
Fasporträttet ger en uppfattning om stabiliteten.
 |
(2.4) |
![`:=`(syst, [(D(x))(t) = eval(f, fcn), (D(y))(t) = eval(g, fcn)])](images/datorle6_32.gif){kind=small}
![[(D(x))(t) = `+`(`*`(`^`(y(t), 2)), `-`(1)), (D(y))(t) = `+`(`*`(`^`(x(t), 3)), `-`(y(t)))]](images/datorle6_33.gif){kind=small} |
(2.5) |
![DEplot(syst, [x(t), y(t)], t = -3 .. 8, [[x(0) = 0, y(0) = `/`(1, 4)], [x(0) = 0, y(0) = `/`(1, 2)], [x(0) = 0, y(0) = `/`(3, 4)], [x(0) = 0, y(0) = 2]], x = -3 .. 3, y = -3 .. 3, arrows = MEDIUM, ste...](images/datorle6_34.gif){kind=small}
![DEplot(syst, [x(t), y(t)], t = -3 .. 8, [[x(0) = 0, y(0) = `/`(1, 4)], [x(0) = 0, y(0) = `/`(1, 2)], [x(0) = 0, y(0) = `/`(3, 4)], [x(0) = 0, y(0) = 2]], x = -3 .. 3, y = -3 .. 3, arrows = MEDIUM, ste...](images/datorle6_35.gif){kind=small}
![DEplot(syst, [x(t), y(t)], t = -3 .. 8, [[x(0) = 0, y(0) = `/`(1, 4)], [x(0) = 0, y(0) = `/`(1, 2)], [x(0) = 0, y(0) = `/`(3, 4)], [x(0) = 0, y(0) = 2]], x = -3 .. 3, y = -3 .. 3, arrows = MEDIUM, ste...](images/datorle6_36.gif){kind=small}
 |
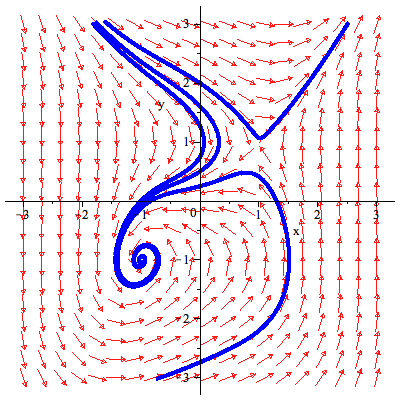Av allt att döma är en punkt asymptotiskt stabil och den andra instabil. Lineariseringen bekräftar detta.
Koefficientmatrisen kan man bilda på följande sätt.
 |
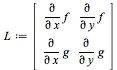
(2.6) |
sätt in jämviktspunkterna
![`:=`(P1, map(eval, L, jmv[1]))](images/datorle6_40.gif){kind=small}
 |
(2.7) |
varefter egenvärdena beräknas
](images/datorle6_43.gif){kind=small} |
(2.8) |
Ett positivt egenvärde ger instabil jämvikt.
![`:=`(P2, map(eval, L, jmv[2]))](images/datorle6_44.gif){kind=small}
 |
(2.9) |
](images/datorle6_47.gif) |
(2.10) |
Båda egenvärdena har negativ realdel. Asymptotiskt stabil jämvikt.