Uppgift 6.4: 20 

restart; -1; with(DEtools); -1 

`:=`(f, y) 

y (5.1)
 

`:=`(g, `+`(`-`(sin(x)), `-`(`*`(`/`(1, 4), `*`(y, `*`(abs(y))))))) 

`+`(`-`(sin(x)), `-`(`*`(`/`(1, 4), `*`(y, `*`(abs(y)))))) (5.2)
 

`:=`(fcn, {x = x(t), y = y(t)}) 

{x = x(t), y = y(t)} (5.3)
 

`:=`(syst, [(D(x))(t) = eval(f, fcn), (D(y))(t) = eval(g, fcn)]) 

[(D(x))(t) = y(t), (D(y))(t) = `+`(`-`(sin(x(t))), `-`(`*`(`/`(1, 4), `*`(y(t), `*`(abs(y(t)))))))] (5.4)
 

DEplot(syst, [x(t), y(t)], t = -3 .. 20, [[x(0) = 0, y(0) = 2]], x = -5 .. 5, y = -3 .. 3, arrows = MEDIUM, stepsize = 0.1e-1, linecolor = [BLUE])
DEplot(syst, [x(t), y(t)], t = -3 .. 20, [[x(0) = 0, y(0) = 2]], x = -5 .. 5, y = -3 .. 3, arrows = MEDIUM, stepsize = 0.1e-1, linecolor = [BLUE]) 

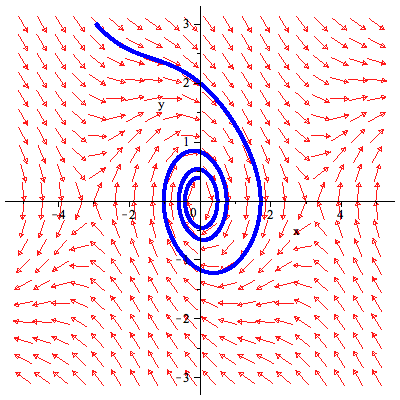Plot_2d
 

Liapunovfunktionen 

`:=`(V, `+`(1, `-`(cos(x)), `*`(`/`(1, 2), `*`(`^`(y, 2))))) 

`+`(1, `-`(cos(x)), `*`(`/`(1, 2), `*`(`^`(y, 2)))) (5.5)
 

har den negativt semidefinita derivatan längs fältet (f,g) 

`:=`(dV, simplify(`+`(`*`(f, `*`(diff(V, x))), `*`(g, `*`(diff(V, y)))))) 

`+`(`-`(`*`(`/`(1, 4), `*`(`^`(y, 2), `*`(abs(y)))))) (5.6)
 

Eftersom den enda lösningen med y = 0 också innebär att x = 0 är jämvikten asymptotiskt stabil.