Frågor och svar gällande tentamina i TATA44:
-
Fråga: jag har en fråga angående skapandet av en rand för olika ytor. I Greens sats så måste de inre ränderna orienterias i motsatt riktning jämfört med den omslutande randen. När jag kollar på gamla tentor så ser de ofta till att den nya randen går i samma riktning som den gamla som känns ointuitivt av Greens. Är detta rätt och hur kan man övertyga sig av det, är detta någon följd av att man inte längre är i 2D utan 3D?
Svar: Man ska ta hänsyn till två viktiga saker: 1) randens orientering och 2) tecken före respektive integralen. Om man väljer "samma" orientering då ska man rätta till tecken före integralen, t ex \[\int_{L_1+L_2}\mathbf{F}\bullet d\mathbf{r}=\int_{L_1}\mathbf{F}\bullet d\mathbf{r}+\int_{L_2}\mathbf{F}\bullet d\mathbf{r}=\int_{L_1}\mathbf{F}\bullet d\mathbf{r}-\int_{(-L_2)}\mathbf{F}\bullet d\mathbf{r}\] etc
Exempelvis, om man har 1D integral (linjeintegral) som \(\int_{\partial D}\mathbf{F}\bullet d\mathbf{r}\) över hela randen \(\partial D\), t ex från Green satsen, så ska man orientera samtliga komponenter av \(\partial D\) i positiv riktning, vilket betyder att du ska ha det inneslutna integrationsområdet på din vänstra sida när du går/löper runt det. Det samma gäller 2D integraler och Stockes/Gauss sats: satserna föreskriver vilken orientering ska gälla. -
Fråga: jag har en fråga angående tentan i TATA44 som gick 2014-10-31, Min fråga handlar om normaler, i t.ex. fråga 3 har vi en kon, vi använder gauss och då skall vi sluta till konen med en cirkelskiva, jag förstår inte varför normalen på den ytan om vi kallar den \(S_1\):
så är normalen = \((0,0,-1)\) men i uppgiften står det att normalen lyder \(n\bullet \hat{z}> 0\). Varför är inte normalen \((0,0,1)\) , då \(S_1\):\( x^2 + y^2 = 1\), \(z=0.\)
Jag har en liknande fråga på uppgift 2 där jag får normalen negativ i alla komponenter, men skall vara positiva.
Svar: Observera att normalens riktning ges i uppgiften för respektive ytan – i ditt fall för konen (säg \(S\)). För att räkna integralen så väljer DU att gå med Gauss, det vill säga, bygger du konen till en sluten yta, i ditt fall m h a en cirkelskiva (säg \(S_1\)). Gauss satsen kräver att normalens riktning ska vara utåtriktad längs HELA sluten ytans yta. Med andra ord, ska DU välja normalens riktning SJÄLV – på de ”ytterligare” ytor (så som \(S_1)\) för att det ska vara kompatibel, dvs utåtriktad. Det förklarar varför ”bottenyta \(S_1\)” har normalensriktning nedåt. -
Fråga: Har en liknande fråga, om man har en uppgift och jag använder stokes, och sen vill jag ta fram en normal till \(S: x^2 + y^2 +z^2 =1\),
och vill ta fram den genom \(r'_\phi \times r'_\theta\) (där \(x,y,z\) är i sfäriska koordinater så får jag negativa komponenter.
Ska det vara så? eller vill man att normalens komponenter ska vara postiva, jag får alltså \(-\sin^2 \theta\cdot \cos \phi\cdot \hat{x} -\sin^2\theta \cdot \sin\phi\cdot \hat{y}\) och
\(-\sin\theta \cdot \cos\theta \cdot\hat{z}\). Jag använder alltså inte ortsvektorn, utan sätter in vad \(x,y,z\) är lika med och deriverar för \(\phi\) och \(\theta\)
Svar: Observera att just tecken i för sig har ingen speciell betydelse, istället ska man kontrollera orientering m.h.a. antigen de villkor som (eventuellt) finns föreskrivna i uppgiften, eller de som finns i motsvarande sats. Det innebär att du inte bara väljer en ytans normal till Stokes, men även normalens riktning (obs! INTE normalens komponenter!), så att normalen ska vara kompatibelt med orientering. Ofta det är så att man räknar normalen utifrån en vis metod, alltså utan ngt samband med orientering. I så fall ska man kontrollera att den hittade normalen uppfyller (eller inte uppfyller) orienteringskrav, och is så fall rätta till den. -
Fråga:
varför är D enkelt sammanhängande i uppgift 4 i
denna tenta?
Svar: \(D\) är \(\mathbb{R}^3\) där planet \(y=0\) är borttagen. D. v. s. består \(D\) av två komponenter, nämligen av två halfrumen (där antigen \(y>0\) eller \(y<0\)). Om \(L\) är an sluten kurva i \(D\) så kan man alltid dra \(L\) till en punkt (eftersom det inte finns några ”hål” eller linjer borttagna, som kunde vara hinder). Däremot blir situationen helt annorlunda om \(D=\mathbb{R}^3\) med villkoret \(x^2+y^2>0\). I så fall är \(D\) lika med \(\mathbb{R}^3\) med \(z\)-axeln \(Z\) borttagen, alltså om \(L\) är en sluten kurva som går ett varv runt om \(Z\) så kan man INTE längre dra \(L\) till en punkt, för att \(Z\) är ett hinder, se bilden nedan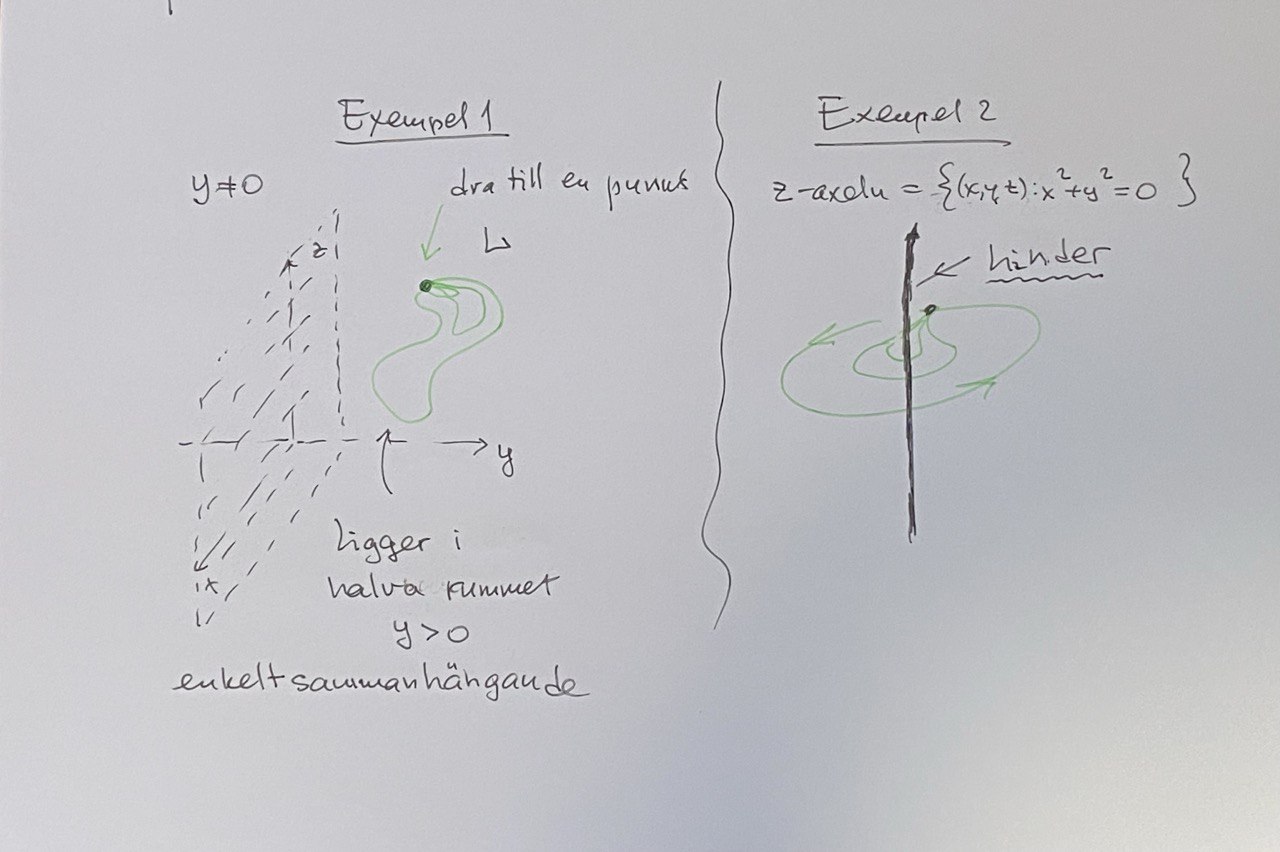
-
Fråga: Vad innebär att rotationen av ett vektorfält är noll.
Svar: Observera att det finns flera olika påståenden:
1) Om ett vektorfält är potentiellt, dvs \(\mathbf{F}=\nabla f(x,y,z)\) så gäller det att \(\mathrm{rot}\, \mathbf{F}=\mathbf{0}\)
2) Om ett vektorfält \(\mathbf{F}\) är rotationfritt, dvs \(\mathrm{rot}\, \mathbf{F}=\mathbf{0}\), i ett enkelt sammanhängande område \(D\) så är \(\mathbf{F}\) potentiellt, dvs existerar en funktion \(f\) sådan att \(\mathbf{F}=\nabla f(x,y,z)\)
\(\rightarrow\) Det betyder att vara potentiellt vs rotationsfritt beror på definitionsmängden till \(\mathbf{F}\), se även Fråga 4 ovan. -
Fråga:
Hur kommer det sig att man ibland när man ska beräkna Ytintegralen skriver man:
1) \(\iint \mathbf{F} \,dS\)
och andra gånger
2) \(\iint \mathbf{F}\bullet \mathbf{n} \,dS\)
Var är skillnaden på dessa två? Och kan man fortfarande använda samma satser på båda ?
Svar: Observera att integralen som du skriver \(\iint \mathbf{F} \,dS\) är en allmän ytintegral där \(dS\) är ett areaelement (ytelement), den motsvarar i boken exakt till formeln (5.8). Här gäller integration av ett vektorfält mot ytelement \(dS\), ingen normal inblandad. Observera också att vi jobbar inte så mycket med den här varianten, men i stället med
3)\(\iint \varphi \,dS\)
som motsvarar (5.9) i boken. Till exempel, om man skulle räkna ytans area så väljer man \( \varphi=1\)
Däremot, den andra integralen \(\iint \mathbf{F}\bullet \mathbf{n} \,dS\) är en flödesintegral, dvs man räknar yterliggare skalär produkt mellan vektorfältet \(\mathbf{F}\) och ytans normal \(\mathbf{n}\). I så fall kan man utnyttja t ex Gauss satsen.
Sidansvarig: vladimir.tkatjev@liu.se
Senast uppdaterad: 2023-10-20
 Homepage
Homepage